Садовничий Ю. Площадь трапеции равна произведению полусуммы ее оснований на высоту Теорема 2. Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь Теорема 3. Площадь параллелограмма равна произведению основания на высоту, опущенную на данное основание, или произведению двух сторон на синус угла между ними Теорема 4. В Четырехугольнике Abcd Ab Cd Bc Ad Докажите Что Треугольник Abd Bcd' title='В Четырехугольнике Abcd Ab Cd Bc Ad Докажите Что Треугольник Abd Bcd' />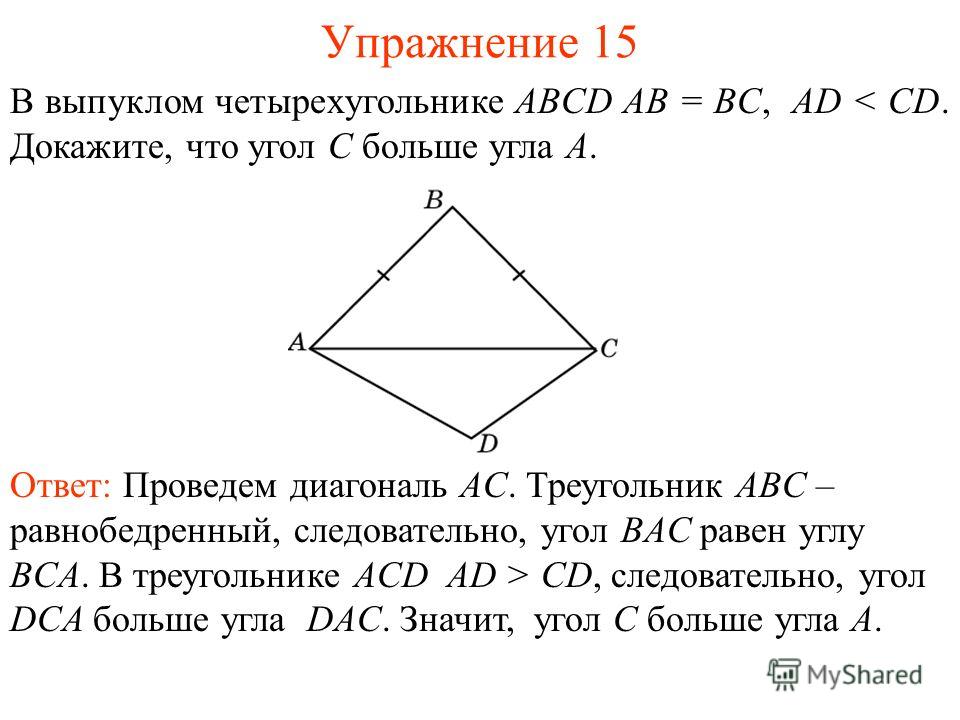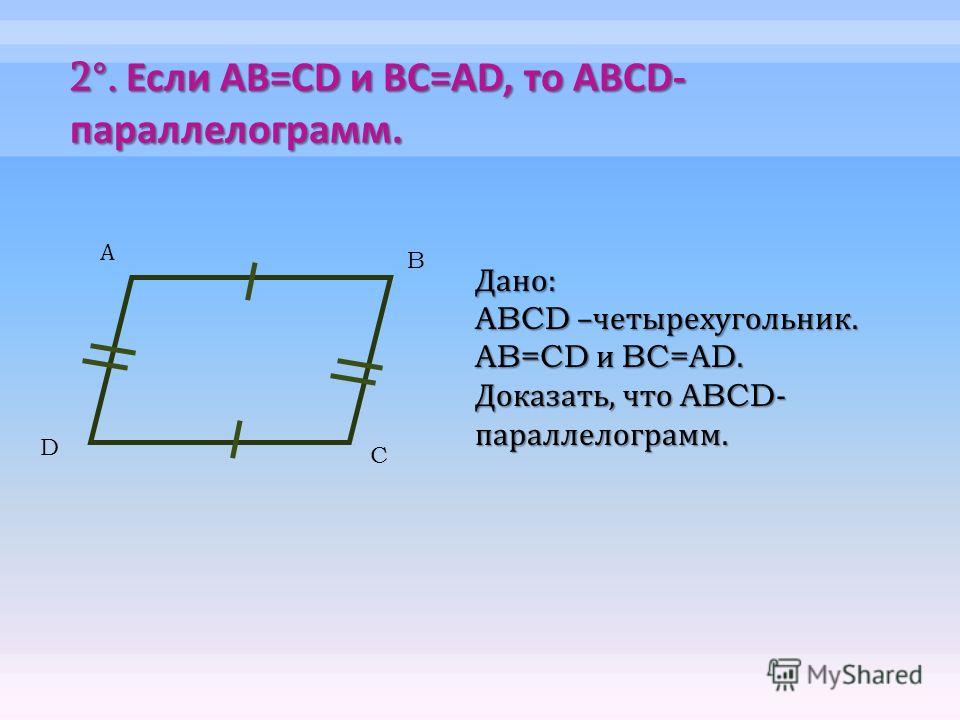В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними Теорема 6. Площадь четырехугольника, описанного около окружности, равна произведению полупериметра этого четырехугольника на радиус данной окружности Теорема 7. Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, есть параллелограмм, площадь которого равна половине площади исходного четырехугольника Теорема 8. Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны AB2 CD2 BC2 AD2. Горки детские, домики, песочницы и многое. Самые низкие. цены, скидки, сжатые сроки изготовления, выезд и консультация специалиста, гарантия. В Четырехугольнике Abcd Ab Cd Bc Ad Ac 20 Bd 10 Ab 131 В четырехугольнике ABCD ABCD,BCAD. Определить является ли четырехугольник трапецией Delphi Привет. Подскажите, как. То есть, если у четырехугольника противоположные стороны равны, то он. Пусть дан четырехугольник ABCD, у которого AB CD и BC AD. Наша группа в контакте httpsvk. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты. Вы сможете на сайте, который располагается по адресу http dkrost. Доказательства некоторых теорем Доказательство теоремы 2. Пусть ABCD  данная трапеция, AD и BC  ее основания, O  точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустим из точек B и C на прямую AD перпендикуляры BP и CQ. В Четырехугольнике Abcd Ab Cd Bc Ad Угол A 30' title='В Четырехугольнике Abcd Ab Cd Bc Ad Угол A 30' />Тогда площадь треугольника ABD равнаа площадь треугольника ACD равна Так как BP CQ, то и S. Но площадь треугольника AOB есть разность площадей тре. Следовательно, площади треугольников AOB и COD равны, что и требовалось доказать. Доказательство теоремы 4. Пусть ABCD  параллелограмм, AB CD a, AD BC b, AC d. BD d. 2,. Применим к треугольнику ABD теорему косинусов Применив теперь теорему косинусов к тре. Пусть ABCD  произвольный выпуклый четырехугольник, E  точка пересечения его диагоналей, AE a, BE b,CE c, DE d,. Имеем что и требовалось доказать. Доказательство теоремы 6. Пусть ABCD  произвольный четырехугольник, описанный около окружности, O  центр этой окружности, OK, OL, OM и ON  перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно. Имеем где r  радиус окружности, а p  полупериметр четырехугольника ABCD. Доказательство теоремы 7. Угол между сторонами AB и CD четырехугольника ABCD равен j. Докажите, что AD2 AB2 BC2 CD2 2AB Четырехугольник ABCD описан около окружности с центром O. Докажите, что. Лучи AB и DC пересекаются в точке P, а лучи BC и AD в точке Q. Пусть AB CD BC AD и прямые AB и CD пересекаются в точке M. Следовательно, O центр окружности, вписанной в четырхугольник ABCD. Пусть ABCD  произвольный выпуклый четырехугольник, K, L, M и N  середины сторон AB, BC, CD и AD соответственно. Так как KL  средняя линия треугольника ABC, то прямая KL параллельна прямой AC и Аналогично, прямая MN параллельна прямой AC и Следовательно, KLMN  параллелограмм. Телефонный Справочник Черкассы Онлайн подробнее. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно, Аналогично, Это значит, что откуда вытекает, что Доказательство теоремы 8. Пусть ABCD  произвольный выпуклый четырехугольник, у которого диагонали взаимно перпендикулярны, пусть E  точка пересечения его диагоналей, AE a, BE b, CE c, DE d. Применим к тре. Около круга описана трапеция с углами при основании. Найти отношение площади трапеции к площади круга. Решение. Пусть ABCD  данная трапеция, AB и CD  ее основания, DK и CM  перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна. Так как треугольник ADK прямоугольный, то. Аналогично, из прямоугольного треугольника BCM находим, что Поскольку в данную трапецию можно вписать окружность, то суммы противоположных сторон равны AB CD AD BC, откуда находим Значит, площадь трапеции есть и искомое отношение равно Ответ Задача 2. В выпуклом четырехугольнике ABCD угол A равен 9. Из вершин B и D на диагональ AC опущены перпендикуляры BE и DF. Известно, что AE CF. Доказать, что угол C прямой. Доказательство. Так как угол A равен 9. Без ограничения общности мы можем считать, что AE lt AF в противном случае следует повторить все нижеследующие рассуждения с заменой точек B и D. Нам достаточно доказать, что. Так както и в частности tg . Далее, имеем откуда получаем, что что и требовалось доказать. Задача 3. Периметр равнобочной трапеции, описанной около круга, равен p. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен. Пусть ABCD  данная равнобочная трапеция с основаниями AD и BC, пусть BH  высота этой трапеции, опущенная из вершины B. Так как в данную трапецию можно вписать окружность, то следовательно, Из прямоугольного треугольника ABH находим, Ответ Задача 4. Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD  в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 3. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD. Решение. Как известно, для произвольной трапеции прямая, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, BM MC и AN ND. Далее, так как в трапеции ABMN и NMCD можно вписать окружность, то. BM AN AB MN,MC ND CD MN. Отсюда следует, что AB CD, то есть трапеция ABCD  равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN x, KM 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая вновь уже использованное выше соотношение. BM AN AB MN. В выпуклом четырехугольнике ABCD точки E, F, H, G являются серединами сторон AB, BC, CD, DA соответственно и O  точка пересечения отрезков EH и FG. Известно, что EH a, FG b, Найти длины диагоналей четырехугольника. Решение. Известно, что если соединить последовательно середины сторон произвольного четырехугольника, то получится параллелограмм. В нашем случае EFHG  параллелограмм и O  точка пересечения его диагоналей. Тогда Применим к треугольнику FOH теорему косинусов Так как FH  средняя линия треугольника BCD, то Аналогично, применив теорему косинусов к треугольнику EFO, получим, что откуда Ответ Задача 6. Боковые стороны трапеции равны 3 и 5. Известно, что в трапецию можно вписать. Средняя линия трапеции делит ее на две части, отношение площадей которых равно Найти основания трапеции. Решение. Пусть ABCD  данная трапеция, AB 3 и CD 5  ее боковые стороны, точки K и M  середины сторон AB и CD соответственно. Пусть, для определенности, AD BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM  средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство Далее, так как в трапецию ABCD можно вписать окружность, то AD BC AB CD 8. Тогда KM 4 как средняя линия трапеции ABCD. Пусть BC x, тогда AD 8 x. Имеем Значит, BC 1 и AD 7. Ответ 1 и 7. Задача 7. Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a, а длина боковой стороны BC равна b. Найти площадь трапеции. Решение. Пусть E  точка пересечения продолжений боковых сторон трапеции и CD x, тогда AD x, AB 2x. Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE BC b и DE AD x, откуда. AE 2x. Итак, треугольник ABE равнобедренный AB AE и AC  его медиана. Поэтому AC является и высотой этого треугольника, и значит,Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия то Ответ Задача 8. Диагонали трапеции ABCD пересекаются в точке E. Найти площадь треугольника BCE, если длины оснований трапеции AB 3. DC 2. 4, боковой стороны AD 3 и угол DAB равен 6.